미분
미분은 '특정 순간'의 변화량이며, 수식은 다음과 같다.

이는 결국 x의 '작은 변화'가 함수 f(x)를 얼마나 변화시키느냐를 의미한다.
이때 시간의 작은 변화, 즉 시간을 뜻하는 h를 한없이 0에 가깝게 한다는 의미를 lim h->0 로 나타낸다.
# 나쁜 구현 예
def numerical_diff(f,x):
h = 10e-50 # 작은 값. 이 방식은 결국 반올림 오차 문제를 일으키게 된다.
return (f(x+h) - f(x)) / h
함수 f의 차분 문제도 있다.
'진정한 미분'은 x 위치의 함수의 기울기(접선)에 해당하지만, 이번 구현에서의 미분은 (x+h)와 x 사이의 기울기에 해당한다.
def numerical_diff(f,x):
h = 1e-4 #0.0001
return (f(x+h) - f(x-h)) / (2*h)
문제점들을 해결한 코드이다.
편미분
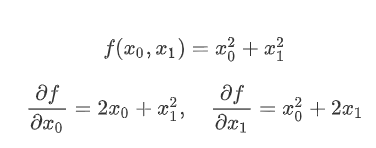
여기선 변수가 2개이기 때문에 '어느 변수에 대한 미분이냐', 즉 x0과 x1 중 어느 변수에 대한 미분이냐를 구별해야 한다.
편미분은 변수가 하나인 미분과 마찬가지로 특정 장소의 기울기를 구한다.
단, 여러 변수 중 목표 변수 하나에 초점을 맞추고 다른 변수는 값을 고정한다.
위 글은 「밑바닥부터 시작하는 딥러닝」을 참고하여 작성한 글입니다.
'Study > Deep Learning' 카테고리의 다른 글
| 머신러닝 Data 종류 (0) | 2021.10.14 |
|---|---|
| 머신러닝 기본 프로세스 (0) | 2021.10.14 |
| 딥러닝의 응용분야 (0) | 2021.10.13 |
| 머신러닝/딥러닝 기초 (0) | 2021.10.13 |
| 신경망 학습 (0) | 2020.11.06 |